NP困難
自分の理解で簡単に書くと、「理論上は解けるが多項式時間では解けないため最適解が得られない問題」ということ。
しかし「解けない」=「お手上げ」では実生活に支障をきたすので、近似値を求めることで利便を保っている。
今回は、巡回セールスマン問題だ。巡回しなければならない地点が複数存在する場合に、どのような経路で回るのが最も小さいコストで回れるかといった問題。
さて、港区赤坂には、19か所の有名な坂がある。
{三分坂, 薬研坂, 丹後坂, 本氷川坂, 南部坂, 稲荷坂, 牛鳴坂, 弾正坂, 氷川坂, 転坂, 円通寺坂, 紀伊国坂, 乃木坂, 檜坂, 新坂, 九郎九坂, 桜坂, 霊南坂, 福吉坂}
この19か所を、最も効率よく巡回したいとする。このときのパターン数は、19! / 2 通り。計算すると、6京822兆5502億441万6000通り。1TFLOPの家庭用コンピュータで計算する場合、約6万秒かかる。およそ16時間。これは待てない。
そこで、妥協した計算方法で近似値を求めたいと考えた。
Kiyonagi Sandbox -19の坂を最も効率よく回る方法を求める-
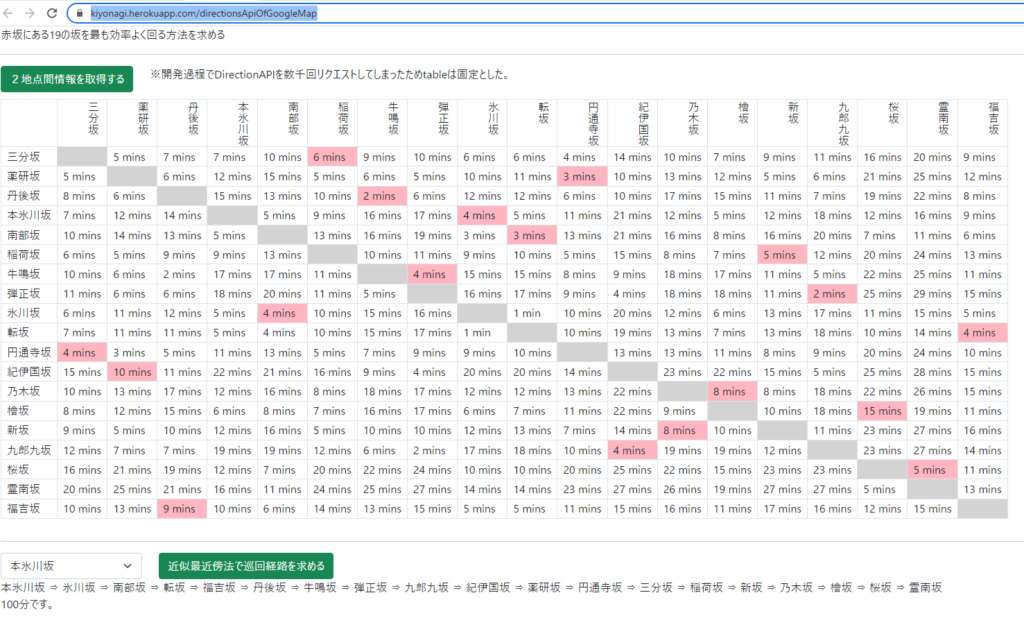
自宅に一番近い本氷川坂をスタート地点とし、近似最近傍法で巡回経路を求め、以下の結果となった。
本氷川坂 ⇒ 氷川坂 ⇒ 南部坂 ⇒ 転坂 ⇒ 福吉坂 ⇒ 丹後坂 ⇒ 牛鳴坂 ⇒ 弾正坂 ⇒ 九郎九坂 ⇒ 紀伊国坂 ⇒ 薬研坂 ⇒ 円通寺坂 ⇒ 三分坂 ⇒ 稲荷坂 ⇒ 新坂 ⇒ 乃木坂 ⇒ 檜坂 ⇒ 桜坂 ⇒ 霊南坂
これで100分だ。
各地点間の距離時間は、GoogleMap Direction API で取得している。
※開発過程で試しすぎて数千リクエストを越えて怖くなったので、ひとまず静的なtableに書き換えてある。
後日、これに沿って19の坂を巡ってこようと思う。